あらゆる検査は間違える（疑陽性・偽陽性とは）

2022年5月11日2022年8月14日

はじめに

現在の日本は、ワクチン推進派とワクチン慎重派（あるいは拒否派）、マスク着用派（あるいは強制派）とマスク拒否派など、双方入り乱れてバトル状態です。

そうした中で、一般市民の一人ひとりが、科学的根拠（evidence）に基づく考え方を強化することが求められています。自らの手で正しい情報を入手して、正しく判断する能力が求められています。

「あらゆる検査は間違える」ことを理解した上で、リスクを最小限に抑えるにはどうしたらよいか、全ての人が自分の頭で考えるべき問題となっています。

記者ハンドブックを確認する

記者ハンドブック（第14版：2022/03/15発行）では、
「ぎようせい」について、以下二つの用語が併記されています。

• 「疑陽性」〔陽性かと疑われる〕
• 「偽陽性」〔誤って陽性とされる〕

2020年以降、新型コロナウイルス感染症の検査をめぐって、「偽陽性」という用語の重要性が増したので、併記することになったものと思われます。

「疑陽性」については、「二つ以上の表記があるもので、その一方を統一的に使うもの、統一用語」であるとして、〈擬陽性→疑陽性〉と注記されています。

旧版（第13版）を確認すると、以下のみが収載されています。

• 「疑陽性」〔説明文無し〕

「疑陽性」は、「文部科学省が制定した学術用語」である、とされていますが、用語の説明は特にありません。また、特に何の説明もなく、〈擬陽性→疑陽性〉とされています。

参考資料

岩田健太郎著『僕がPCR原理主義に反対する理由』
集英社インターナショナルe新書、2020/12/7刊

幻想と欲望のコロナウイルス（副題）
検査万能主義に陥っている日本人に送る、警告の書！（帯のキャッチコピー1）
ファクターXという幻、そしてPCR検査への誘惑を絶つ！（帯のキャッチコピー2）

上記、岩田健太郎さん（医師：神戸大学医学研究科感染症内科教授）そのほかを参考にしながら、「検査」について、まとめてみることにしました。

岩田さんは、「（臨床）検査」というものに対して、一般の方には、以下のことをざっくりとでも理解してもらえれば十分としています。

「病気ではない人が陽性と判定されることもあれば、病気の人が陰性だと判定されることもある。それはあらゆる検査で避けられないことだ」。

この後で、検査をめぐって、幾つかの概念が出てきますが、岩田さんによれば、「医学生でもきちんと理解できていない人がたくさんいます。僕自身も腑（ふ）に落ちるまでは何年もかかりました」（岩田2020,p.73）ということです。

定性抗原検査キットでスクリーニングはできない

定性抗原キットの感度は、PCR検査キットと比べて劣る

感度63％（PCR陽性、抗原検査も陽性）
　　PCR陽性（発症例）、抗原検査も陽性、77.8％
　　PCR陽性（発症無し）、抗原検査も陽性、39.2％
特異度99.8％（PCR陰性、抗原検査も陰性）

対象：米国スタンフォード大学の学生
キット：BinaxNOW（Abbott Laboratories社製）

Jessica Tsao, MD; Andrea L. Kussman, MD; Cristina Costales, MD; et al
JAMA Netw Open. 2022;5(6):e2217234. doi:10.1001/jamanetworkopen.2022.17234

事前確率60.0％（周囲の2人に一人以上は感染している状況）の場合：

◎新型コロナウイルスに感染しているにもかかわらず、抗原検査キット（－）例が、37％もある。

A＋B（感染している人数）＝1,000,000×60.0％（事前確率）→600,000人
A＝600,000人×63％（感度）→378,00人（真陽性）
B＝600,000人×37％→222,000人（偽陰性）

◎新型コロナウイルスに感染していないにもかかわらず、抗原検査キット（＋）例が、約0.2％ある。

C＋D（感染していない人数）＝1,000,000-600,000＝400,000人
C＝400,000×99.8％（特異度）→399,200人（真陰性）
D＝400,000×0.2％→800人（偽陽性）

◎コロナ（＋）の患者を、コロナ（ｰ）と間違って判断する確率が、約35.7％（約1/3）もある。

陰性的中率は、約64.3％である（下記より）。
つまり、陰性の結果が得られた中で、実際に疾患を有しない場合が、約64.3％あることを示している。
裏返して考えると、実際に疾患を有するにも関わらず、陰性の結果が得られた場合が、
（1-0.643）＝35.7％あることが分かる。

C／（B＋C）：陰性的中率
＝399,200/（222,000+399,200）→約64.3％（≒0.6426）
A／（A＋D）：陽性的中率
＝378,000/（378,000+800）→約99.8％（≒0.9979）

ツベルクリン反応とBCG（疑陽性：疑い陽性／陽性かと疑われる）

「結核はわが国の主要な感染症の一つです。毎年新たに1万8,000人程度の患者が発生しており、日本は結核の低まん延国ではありません」。

厚生労働省／結核とBCGワクチンに関するQ&A
https://www.mhlw.go.jp/seisakunitsuite/bunya/kenkou_iryou/kenkou/kekkaku-kansenshou/bcg/index.html

ツベルクリン反応検査（ツ反）

ツベルクリンは、結核菌感染の診断に用いられる抗原です。つまり、ツベルクリン反応検査は、結核菌感染の有無を知る検査法の一つです。

ツベルクリン（定義）とは、「牛型結核菌及び人型結核菌の培養ろ液を濃縮して調製した皮内反応用抗原、又は牛型結核菌の培養ろ液を精製して調製した皮内反応用抗原」です。

ツベルクリン反応とは、ツベルクリンを皮内注射すると、皮内で免疫反応が起こり、皮膚に発赤、硬結（しこり）などができることを言います。日本では、投与48時間後に投与部位の発赤を測定して、感染があるかどうか（免疫があるかどうか）を診断します。

私たちの子どもの頃には、発赤長径が0～4㎜を「陰性」、10㎜以上を「陽性」（この中をさらに3段階に区分）とするほかに、「疑陽性」（5～9㎜）というのがありました。（全部で5段階）

• 陰性：発赤長径0～4㎜
• 疑陽性：同5～9㎜
• 陽性：同10㎜以上（さらに3段階に区分）

「疑陽性」とは、まさに、陽性かと疑われる「疑い陽性」のことであり、陽性であるかどうか「疑って」いるのです。

そして、ツ反「陰性」（発赤長径が0～4㎜）ならば、結核に感染していない（免疫ができていない）として、結核予防のため、BCGワクチンを接種しました。

資料によれば、私たちの頃には、「疑陽性」（発赤長径が5～9㎜）でもBCGワクチンを接種した、となっています。ただ、私にはその記憶がありません。

私の記憶にあるのは、「お前は疑陽性だから、海に入ってはいけない」と言われていたことだけです。小学校に上がる前だったと思うのですが、私は海で遊ばせてもらえませんでした。海に入れなかった理由は、まだ結核に感染していないからということだったのでしょうか。

なお、その後、日本での結核感染者数の減少に伴い、ツ反は廃止されました。ツ反を実施せず、最初からBCGワクチンを打つ直接接種に変更されたのです。また、ワクチン接種の年齢層も低下しています。

平成25年度（2013年度）以降は、生後1歳に至るまでの間に、１回接種することに変更されました。（標準的な接種は、生後5か月から8か月の間とされている）

BCGワクチン

「結核の予防に用いるBCG（Bacillus Calmette-Guerin）はその名の通り、Bacillus(細菌)とこれを作った2人の名前（CalmetteとGuerin）をとって名づけられています。BCGワクチンは乳幼児を中心として結核予防のために世界各国で使われています」。Web作者注）Bacillus属の細菌を使うという意味。

BCGを作った男たち　アルベール・カルメットとカミーユ・ゲラン
https://www.bdj.co.jp/safety/articles/ignazzo/hkdqj2000005sivo.html

年代別予防接種早見表（BCG 1回（現在））

・1951年～ 1967年 法律による皮内接種。ツ反陰性者、擬陽性にBCG接種
・1967年～ 経皮注射に変更
・1974年 0～４歳まで、小、中で計3回、ツ反陰性者にBCG接種
・1982年 2回目を中2から中１へ変更
・1995年～ ツ反９mm以下に接種変更
・2003年 小中へのツ反検査とBCG再接種廃止、4歳未満へBCG接種
・2005年 ツ反せずに６か月までBCG一回接種
・2013年～ １歳までにBCG一回接種

一般社団法人 安佐医師会
http://www.asaishikai.jp/tayori/tayori18.html

PCR検査（偽陽性：誤って陽性とされる）

PCR（polymerase chain reaction：ポリメラーゼ連鎖反応)とは、生物の遺伝情報を持つDNAを複製して、増幅させるための原理のことを言います。

実用例としては、DNA鑑定や新型コロナウイルス（SARS-CoV2）の検出などがあります。

PCR検査では、検体に含まれるごく微量のDNA（あるいはRNA）断片を用いて、特定の塩基配列部分を急速に増幅した上で、判定を行います。必要な検体量としては、現在では、フェムトモル（1000兆分の1モル）程度のDNAがあれば、検出容易な程度にまで増幅が可能だとされています。

検査結果に、誤り（偽陽性・偽陰性）は避けられない

「偽陽性」とは、真の陰性患者を「陽性」と「偽る（いつわる）」こと、つまり、真の陰性患者を〈誤って陽性〉と判断することを言います。

「偽陰性」とは、真の陽性患者を「陰性」と「偽る（いつわる）」こと、つまり、真の陽性患者を〈誤って陰性〉と判断することを言います。

検査の正確性は、感度と特異度で判断する

感度と特異度は、検査の正確性を図る指標です。

• 感度＝真陽性／感染者数＝a/（a+c）

  陽性と判定されるべきものを、正しく陽性と判定する確率
  疾患がある人の中で、検査が正しく陽性と判断した人の割合
  病気の人を病気だと正しく判断する能力のこと（病気を見逃さない能力のこと）

  ここでは、陰性と判定する（間違える）確率を、できるだけ低く抑えたい

• 特異度＝真陰性／非感染者数＝d/（b+d）

  陰性と判定されるべきものを、正しく陰性と判定する確率
  疾患がない人の中で、検査が正しく陰性と判断した人の割合
  病気でない人を病気でないと正しく判断する能力のこと
  ここでは、陽性と判定する（間違える）確率を、できるだけ低く抑えたい

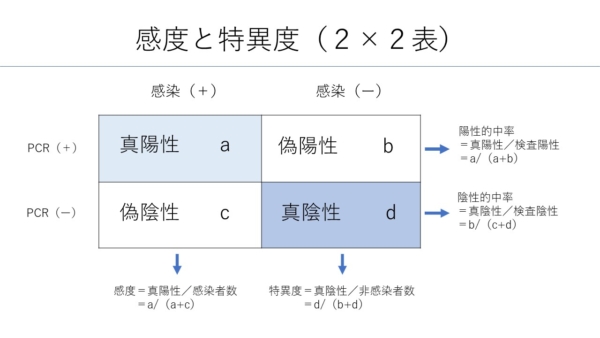
• 真陽性：新型コロナウイルスに感染に感染していて、検査の結果が陽性
• 偽陽性：新型コロナウイルスに感染していないにもかかわらず、検査の結果が陽性
• 偽陰性：新型コロナウイルスに感染しているにもかかわらず、検査の結果が陰性
• 真陰性：新型コロナウイルスに感染しておらず、検査の結果が陰性
• 感度：真陽性の人数／感染ありの人数＝真陽性／（真陽性＋偽陰性）
• 特異度：真陰性の人数／感染なしの人数＝真陰性／（偽陽性＋真陰性）
• 陽性的中率：真陽性の人数／検査で陽性の人数＝真陽性／（真陽性＋偽陽性）
• 陰性的中率：真陰性の人数／検査で陰性の人数＝真陰性／（真陰性＋偽陰性）

PCR検査の感度は約70％程度である

新型コロナウイルス感染症に対するPCR検査では、感度約70％、特異度約95％程度です。
（下記、岩田さん紹介の文献より）

Woloshin S, Patel N, Kesselheim AS. False Negative Tests for SARS-CoV-2 Infection ? Challenges and Implications. The New England Journal of Medicine. 2020 Jun 5; 0( 0): null.

これは、新型コロナウイルスに感染している人が、10人いたとすると、そのうちの3人は感染していない、と誤って判断されることを意味しています。つまり、10人中3人の感染を見逃してしまうことになります。

このように、検査結果とは意外とあいまいなもののようです。
岩田さん自身の感触としても、感度約70％を妥当としています。

そもそも、検査に100％はあり得ません。
極端な話、検体の取り違えだって起こる可能性があります。
あるいは、感染が治った後に残っていたウイルスの残骸を拾ってくることもあります。
それら全ての条件を加味して、感度（確からしさ）70％となっているのです。

感度と特異度はトレードオフの関係にある（閾値の問題）

感度約70％では不満だ、ということになれば、検査精度をもっと上げる必要が出てきます。

例えば、ある基準として、「一万個以上のウイルス遺伝子が検体から見つかれば陽性」とされているとします。それを、「1,000個以上のウイルス遺伝子が見つかれば陽性」と変更すれば、「本当に病気の人」を見逃してしまう確率は、理論的には下がります」。（岩田2020,p.72）

この場合、感度を上げるために、閾値（いきち、しきいち）を下げています。ところが、閾値を下げると、特異度も下がってしまうのです。感度を上げると、特異度は下がります。感度と特異度はトレードオフの関係にあるのです。

特異度とは、病気でない人を病気でないと正しく判断する確率のことです（既述）。したがって、特異度が下がれば、病気でない人を病気と誤って判断する確率が高まります。病気と言われたけれども、実は病気ではなかったというケースが増えてしまいます。

参考）偽陽性の割合＝1から特異度を引いた数（岩田2020,p.73）

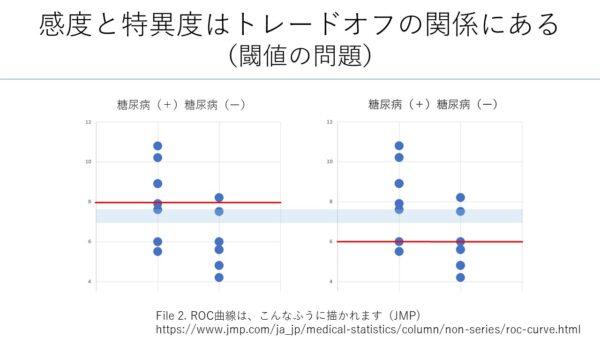
糖尿病とHbA1c（ヘモグロビンA1c）との関係で見てみましょう。

参考）上図のデータは、JMPからお借りしました。
糖尿病の人（8例）、糖尿病でない人（8例）、合計16例です。
異なる人同士で同一データの場合が複数例あり、見た目のデータ数は少なくなっています。

さて、糖尿病と診断された人とそうでない人を比べると、糖尿病の人の方が、HbA1cが高い傾向にあることは確かです。ただし、糖尿病でない人の中にも、HbA1cが高い人はいます。どの値を基準にすれば、糖尿病とそうでない人をきれいに分けることができるでしょうか。

HbA1cのカットオフ値（閾値）8.0と6.0の場合で比べてみます。

左）カットオフ値=8.0
「糖尿病：HbA1c≧8.0」とすれば、糖尿病でない人のほとんどを除外することができます。
しかし、その場合、糖尿病の人のほぼ半数が、糖尿病でないと誤って判断されてしまいます。

右）カットオフ値=6.0
「糖尿病：HbA1c≧6.0」とすれば、糖尿病の人のほとんどを糖尿病と判断することができます。
しかし、その場合、糖尿病でない人のほぼ半数が、糖尿病と誤って判断されてしまいます。

いずれにせよ、糖尿病とそうでない人を、完璧に二分することはできないことは明らかです。
ある程度うまく分割するには、カットオフ値（閾値）をHbA1c=7.0前後にするとよさそうです。

JMPでは、カットオフ値を、以下のように定義しています。
カットオフ値：「感度 – （1 – 特異度）」＝（感度＋特異度-1）が最大になるポイント
上記の場合を計算すると、HbA1c=7.6になります。（Youden Index、参考：ROC曲線）

全ては事前確率で決まる

全例PCＲ検査をすればよい、というものではない

新型コロナウイルス感染症が出現しはじめ頃、医療機関の受け入れ体制が整っていなかったことから、PCR検査の実施数を、意図的に抑えていたと言われたことがあります。

必要十分なベッド数や検査体制を整えることは必須です。
しかしながら、ただやみくもに全例PCR検査をすればよい、というものでもありません。
ここでは、そのことを考えてみることにします。

実は、PCR検査の価値も意味も、その時々の感染状況によって、大きく変わってくるのです。
そして、その時々の感染状況を、「事前確率」という概念で表すことができます。

例えば、100万人中100人だけ感染している場合、事前確率は0.01%にしか過ぎません。
これが、100万人中60万人も感染してしまうと、事前確率は60％にも跳ね上がります。
（もちろん、この事前確率は、推定値ということになります）

以下では、PCR検査の感度90％、特異度99.9％という検査キットを想定しています。
とても優秀な検査キットだと言えるでしょう。

事前確率0.01％の場合（百万人中100人が感染している）

事前確率が0.01％の場合、PCR陽性であっても、実際に感染している確率は約8.3％に過ぎない。

ほとんど感染が広まっていない状態の場合（事前確率0.01%←感染者数100人／百万人）、
PCR陽性患者（真陽性）よりも、PCR偽陽性（感染していないにもかかわらず陽性となる）の方が圧倒的に多くなる。したがって、PCR検査のみで、感染患者を見つけ出す確率は、非常に低くなる。

A＋B（感染者数）＝1,000,000×0.01％（事前確率）→100人
A＝100人×90％（感度）→90人（真陽性）
B＝100人×10％→10人（偽陰性）

C＋D（感染していない人数）＝1,000,000-100＝999,900人
C＝999,900×99.9％（特異度）→998,900人（真陰性）
D＝999,900×0.1％→1,000人（偽陽性）

A／（A＋D）：陽性的中率
＝90/（90+1,000）→約8.3％（≒0.08256）

百万人中100人が感染しているという状況下では、
PCR検査（上記の場合、感度90％）で真陽性となるのは、90人である。
それに対して、偽陽性が1,000人も発生してしまう。

このように、ほとんどの人が感染していないという状況下では、
いかに精度の高い検査キット（上記の場合、特異度99.9％）を用いても、
大量の偽陽性が検出されるため、検査の意味がなくなってします。

事前確率0.1％の場合（百万人中1,000人が感染している）

事前確率が0.1％の場合、PCR陽性であっても、実際に感染している確率は約47.4％に過ぎない。

A＋B（感染者数）＝1,000,000×0.1％（事前確率）→1,000人
A＝1,000人×90％（感度）→900人（真陽性）
B＝1,000人×10％→100人（偽陰性）

C＋D（感染していない人数）＝1,000,000-1,000＝999,000人
C＝999,000×99.9％（特異度）→998,001人（真陰性）
D＝999,000×0.1％→999人（偽陽性）

A／（A＋D）：陽性的中率
＝900/（900+999）→約47.4％（≒0.4739）

事前確率1.0％の場合（百万人中1万人が感染している）

事前確率が1.0％の場合、PCR陽性ならば、実際に感染している確率は約91.0％である。

A＋B（感染者数）＝1,000,000×1.0％（事前確率）→10,000人
A＝10,000人×90％（感度）→9,000人（真陽性）
B＝10,000人×10％→1,000人（偽陰性）

C＋D（感染していない人数）＝1,000,000-10,000＝990,000人
C＝990,000×99.9％（特異度）→989,010人（真陰性）
D＝990,000×0.1％→990人（偽陽性）

A／（A＋D）：陽性的中率
＝9,000/（9,000+900）→約90.9％（≒0.9090）

事前確率10.0％の場合（百万人中10万人が感染している）

事前確率が10.0％の場合、PCR陽性ならば、感染している確率は約99.0％である。

A＋B（感染者数）＝1,000,000×10.0％（事前確率）→100,000人
A＝100,000人×90％（感度）→90,000人（真陽性）
B＝100,000人×10％→10,000人（偽陰性）

C＋D（感染していない人数）＝1,000,000-100,000＝900,000人
C＝900,000×99.9％（特異度）→899,100人（真陰性）
D＝900,000×0.1％→900人（偽陽性）

A／（A＋D）：陽性的中率
＝90,000/（90,000+900）→約99.0％（≒0.9900）

事前確率60.0％の場合（百万人中60万が感染している）

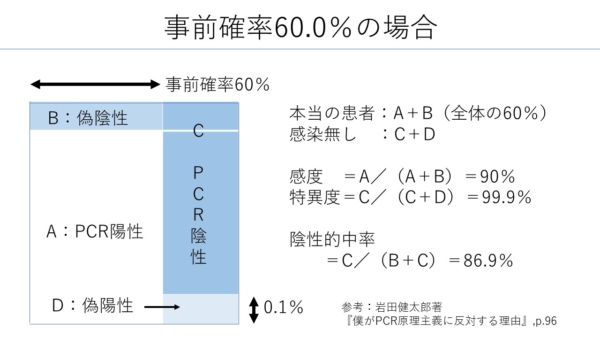
事前確率が60.0％の場合、PCR陽性ならば、感染している確率は約99.9％である。

事前確率が60.0％の場合、PCR陰性ならば、感染していない確率は約86.9％である。
逆に言えば、PCR陰性でも、感染している確率が約13.1％あることになる。
事前確率が60.0％の場合、PCR陰性ならば、再検査は必須とすべきか。

A＋B（感染者数）＝1,000,000×60.0％（事前確率）→600,000人
A＝600,000人×90％（感度）→540,000人（真陽性）
B＝600,000人×10％→60,000人（偽陰性）

C＋D（感染していない人数）＝1,000,000-600,000＝400,000人
C＝400,000×99.9％（特異度）→399,600人（真陰性）
D＝400,000×0.1％→400人（偽陽性）

C／（B＋C）：陰性的中率
＝399,600/（60,000+399,600）→約86.9％（≒0.8694）
A／（A＋D）：陽性的中率
＝540,000/（540,000+400）→約99.9％（≒0.9992）